Datové struktury
Pole (Array)
- Nejjednodušší datová struktura
- Statické (pevná velikost)
- Prvky uloženy v paměti hned za sebou
Plusy a mínusy pole
+ Jednoduché na vytvoření
+ Jednoduché na použití
- Složité vyhledávání
- Složité třídění
- Dlouhé vyhledávání
- Obtížné odstranění prvku
List
- Dynamické (může měnit velikost)
- Vlastnosti podobné jako v pole
- Výhodu oproti poli je snazší práce s daty
Množina
- Všechny prvky jsou unikátní (vyskytují se pouze jednou)
Plusy množiny
+ Rychlá kontrola, jestli obsahuje prvek
+ Bez duplicitních hodnot
Fronta
- anglicky: buffer, queue
- FIFO (First In, First Out) => jako by se zařadil do fronty
->|3|5|4|2|->
Přidání / získání prvku do / z Fronty
// volá funkci
Fronta.add(x)
// funkce:
pole[pocet] = x;
pocet++;
// volá funkci:
Fronta.get()
// funkce:
pocet--;
return pole[pocet];
Zásobník
- anglicky: stack
- LIFO (Last In, First Out) => jako by se zařadil na vrchol
prvek 2 by se po přidání první odebral
->|2|4|5|3|
<-|2|4|5|3|
Přidání / získání prvku do / z Zásobníku
// volá funkci
Zasobnik.get();
// funkce:
pom = pole[0];
for (int i = 1; i < pocet - 1; i++)
{
pole[i] = pole[i + 1];
}
pocet--;
return pom;
Plusy a mínusy fronty a zásobníku
+ rychlé přidání, odebrání a zobrazení prvků
- nemožnost ukládat doprostřed
Spojový seznam (link-list)
Dělí se na tři:
- jednosměrný => Každý prvek nese informaci o tom, kde je následující prvek.
- obousměrný => každý prvek informaci o tom, kde je předchozí a další prvek.
- kruhový => je jednosměrný kde poslední prvek odkazuje na první.
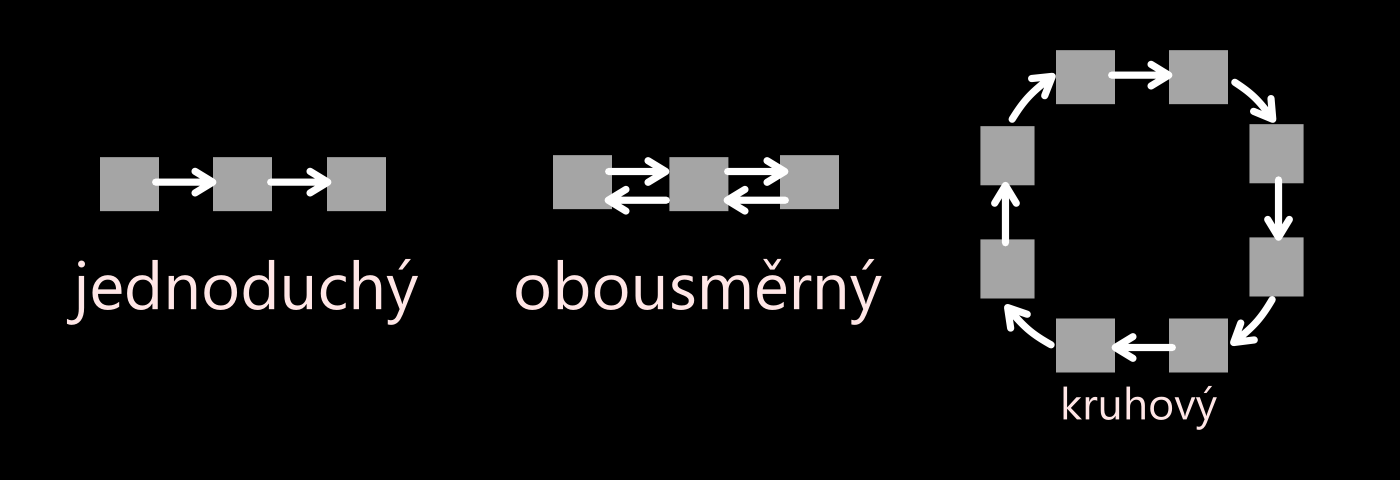
- Prvky oproti poli jsou v paměti rozmístěni různě
Plusy a mínusy spojového seznamu
+ Přidání / odebrání prvků, pouze o změně referencí / pointrů (šipek).
- Složitý a zdlouhavý výpis.
Binární stromy
Stromové struktury, které mají kořen a u každého uzlu mají dva potomky => dva -> binární
Halda (Heap)
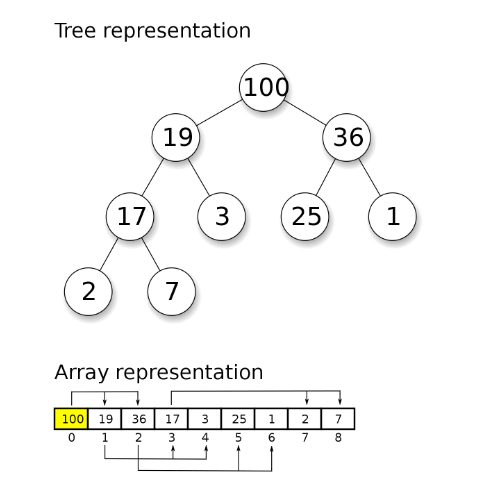
- Nejvyšší prvek je vždy nejmenší / největší
- Každý prvek má nižší/vyšší nebo stejnou hodnotu jako jeho rodič
- Kořen/vrchol obsahuje vždy max/min
- Je to vyvážený binární strom – je téměř celý naplněný
ABC Pravidlo
A > B, C
--------
A < B, C
Plusy a mínusy haldy
+ Velmi rychlé hledání minima a maxima
+ Rychlé přídavní prvků
+ Rychlé odebírání maxima / minima
- Pomalé vyhledávání
- Komplikované odstranění prvku
- obsahuje velké množství jednopotomkových uzlů (nepočítá se poslední/dolní patro)
- extrém (obr.2) = spojový seznam
Vyvážený vyhledávací binární strom (BST = Binary Search Tree)
- vyjma posledního patra neobsahuje jednopotomkové uzly
- oproti haldě je přesně dané, kde který prvek leží
- vpravo je vždy větší prvek a vlevo menší než hodnota uzlu
Proces vyhledávání
např.: 7
5 ≠ 7, ale 7 > 5 → vpravo
8 ≠ 7, ale 7 < 8 → vlevo
6 ≠ 7, ale 7 > 6 → vpravo
7 = 7 → našli jsme!
Strom má 11 prvků, nalezli jsme ve 4 krocích!
Plusy a mínusy vyváženého
+ umožňuje prvky rychle vyhledávat a optimalizuje jejich vkládání a mazání
- složitější manipulace s prvky
Samovyvažovací stromy
- před vytvořením stromu je nejlepší zamíchat prvky => vyvážený strom
- během „života může strom degradovat na nevyvážený až spojový seznam
- řešením jsou Samovyvažovací stromu = mají metody na kontrolu a následné napravení
B-Stromy
- v uzlu může být více prvků
- vytvořeny pro efektivní využití na pevných discích, kdy lze v jednom kroku pracovat s více prvky najednou
- prakticky využívány v databázových systémech
- časové složitosti vycházejí stejně jako binární stromy
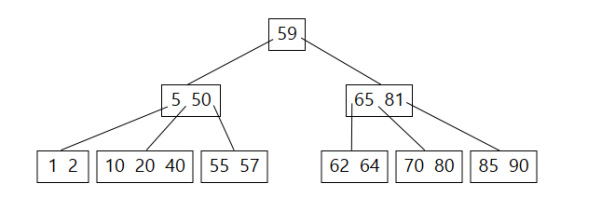
B-Strom není Binární strom!